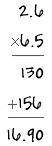Dividing is one of the four basic operations with the other ones being addition, subtraction, and multiplication. However, for most math students, dividing is the most challenging one.
The truth is that overall speaking about the dividing operation, you need to keep in mind that you have to use both subtract and multiplication in order to divide. Besides, you still need to be really good estimating and rounding. So, it’s not much of a big surprise that division is the most complicated operation for students, especially when they are getting started.
One of the reasons why so many students struggle with division is because most of the problems don’t come out even and nice. In fact, they need to think when they are dividing.

The reality is that a lot of math students believe that since they can use a calculator, that this won’t be a problem for them. However, we believe that it is very important to know how to perform all the basic four operations. And the truth to be said, you may use divisions a lot more that you notice.
Just think of the times when you go to a restaurant for lunch with your co-workers. When it is time to pay the bill, you need to divide the check for all. So, you need to know how to divide.
While dividing is already complicated for a lot of students when they are still using whole numbers, when they need to start dividing decimals by a decimal, things can get bad pretty fast. However, there’s really no need for this to occur. To ensure that you can keep track of what we are about to explain to you, we will start by showing you how you can easily divide whole numbers first and then we will move on to dividing decimals by a decimal.
Discover how to round to the nearest hundredth.
Dividing Whole Numbers
As you already know, dividing whole numbers is the opposite of multiplying whole numbers. Simply put, when you are dividing, you want to find out how many times a number (divisor) is contained in another number (dividend).
The answer in the division problem is called a quotient. In the division problem 63 ÷ 7, 7 is contained into 63, 9 times. (9 × 7 = 63)

While this is pretty simple, things can become a bit more complicated when the dividend is bigger than 100. When this occurs, you will need to do a long division.
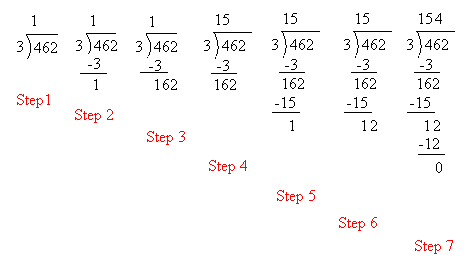
Let’s say that you want to 462 ÷ 3:
Looking to round to the nearest whole number?
It is not easy to see immediately how many times 3 is contained into 462. It may not be easy also to see how many times 3 is contained into 46. However, it is fairly easy to see that 3 is contained into 4 once.
Therefore, we do this in step 1 and put the 1 above the 4.
In step 2, we multiply 1 by 3 and subtract the answer(3) from 4.
In step 3, we bring down the 62. Now, we need to find out how many times 3 is contained in 162. Still, it may not be obvious, so we will try to find out instead how many times 3 is contained into 16.
This is done in step 4 and we see that 3 is contained into 16, 5 times. We put the 5 above the 4.
In step 5, we multiply 5 by 3 and subtract the answer (15) from 16.
In step 6, we bring down the 2.
In step 7, we try to find out how many times 3 is contained into 12.
3 × 4 = 12, so 3 is contained into 12, 4 times.
Finally, we put the 4 above the 6.
The answer is 154. or 3 is contained into 462, 154 times
Now that you already understand how to divide whole numbers, it is time to learn how to divide decimals.
Check out how to round to the nearest tenth.
Dividing Decimals By A Decimal
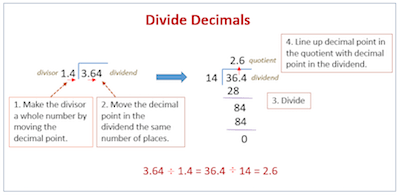
One of the things that it is important to keep in mind when you are dividing decimals is that it is almost the same as dividing whole numbers. The main difference is that you use the position of the decimal point in the dividend to determine the decimal places in the result.
Learn more about how to divide decimals.
So, when you want to divide decimal numbers, you need to follow the next steps:
Step #1: If the divisor is not a whole number:
- Move the decimal point in the divisor all the way to the right (to make it a whole number).
- Move the decimal point in the dividend the same number of places.
Step #2: Divide as usual.
If the divisor doesn’t go into the dividend evenly, add zeroes to the right of the last digit in the dividend and keep dividing until it comes out evenly or a repeating pattern shows up.
Step #3: Position the decimal point in the result directly above the decimal point in the dividend.
Step #4: Check your answer: Use the calculator and multiply the quotient by the divisor. Does it equal the dividend?
Here’s a practical example: 16.9 ÷ 6.5
The first thing that you need to do is to show the division like this:
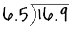
Now move the decimal point one place to the right, which makes the divisor a whole number. Also, move the decimal point in the dividend one place to the right:
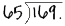
Divide as whole numbers. 65 goes into 169 two times with 39 left over:
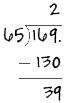
To continue dividing, add a zero to the right of the decimal point in the dividend. Then bring down the zero, and add it to the end of 39, making it 390
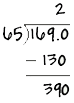
65 goes into 390 six times. We write a 6 above the zero in the quotient and put the decimal point just above the decimal point in the dividend:
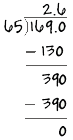
To check our answer, we multiply the quotient by the divisor and make sure it equals the dividend: