If you are new or just entering the electronics and computing industry, then you may be surprised by some things that you never saw before in any level of detail. One of these things is rounding or, more specifically, the rounding algorithm.
Learn everything you need to know about rounding.
Rounding Numbers

Imagine that you have a series of values such as 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, and 5.9, and your goal is to end up with integer values.
If you remember what you were taught in school, then you need to start with the concept of round towards the nearest. In this case, it refers to rounding to the nearest integer.
So, in this simple example, 5.1, 5.2, 5.3, and 5.4 will round to 5, while 5.6, 5.7, 5.8, and 5.9 will round to 6. But what do you do with the “half-way” 5.5 value?
The truth is that it can go either way – either up or down. It ultimately depends on the rounding algorithm that you want (or have to) use. You can either use the “round-half-down” or the “round-half-up” algorithm. However, and going back to school again, you were taught the round-half-up approach, which is also known as “arithmetic rounding”.
How to round to the nearest thousand?
While this is a very simple concept, what happens when you need to round a negative number?
But this isn’t the only question that comes to the mid of many students who are learning the rounding algorithm for the first time. For example, if halfway values are always rounded upward – if 5.5 rounds to 6 and 6.5 rounds to 7, for example – then this can result in a bias that increases as more and more rounding operations are performed. This leads us to the “round-half-even” algorithm, in which halfway values are rounded toward the nearest even number, so 5.5 will round up to 6, while 6.5 will round down to 6. This is often referred to as “banker’s rounding,” because it is commonly used in financial calculations.
Rounding = Less Precision
One of the things that you need to always keep in mind is that while rounding numbers can be very useful and a very practical tool, you always end up with less precision.
For example, suppose that you average out a range of prices and end up with a dollar value of $5.19286. In this case, rounding the more precise value of $5.19286 to the nearest cent would result in $5.19, which is more useful, but less precise.
This is how you round to the nearest hundred.
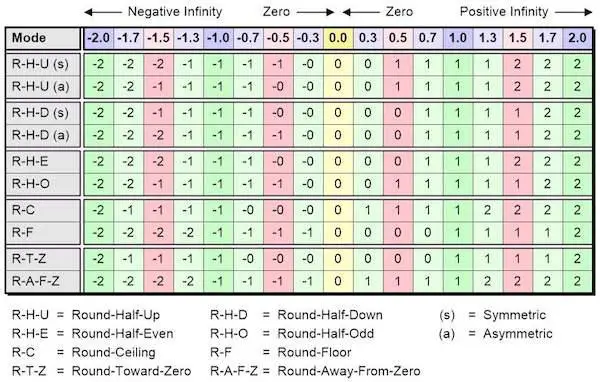
So, this means that if you need to use a rounding algorithm, you need to use one that minimizes the effects of this loss in precision. But the reality is that there isn’t the best rounding algorithm all the time or for all occasions. It depends on your goal. So, we end up with a plethora of rounding algorithms, whose effects may be summarized as shown in the following illustration:
Use our calculator to round to the nearest tens.
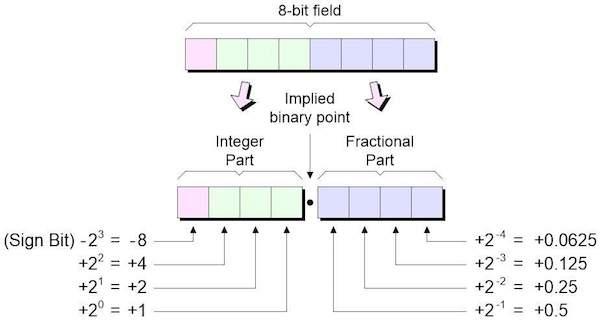
But this is not all… There’s one thing that is common to all the above numbers – they are all sign-magnitude decimal values. But what if you need to work with sign-magnitude binary values? Or how about rounding signed (twos-complement) binary values in the format illustrated below, for example?