Rounding numbers is something that we do every day and we don’t even realize it.
Simply put, the word rounding means replacing a numerical value with another value that is approximately simpler, shorter, or more explicit. For example, $23.74 could be rounded to US$24 as well as the fraction 312/937 could be rounded to 1/3.
Discover everything you ned to know about rounding numbers.
Ultimately, the main purpose of rounding a number is to get a value that is easier to write and handle than the original. Notice that this can also be done to indicate the accuracy of a computed number. For example, a quantity that was computed as 123,456, but is known to be accurate only to within a few hundred units, is better stated as “about 123,500”.
On the other hand, rounding can introduce some round-off error as a result. Rounding is almost unavoidable in many computations, especially when dividing two numbers in integer or doing fixed-point arithmetic, when computing mathematical functions such as square roots, logarithms, and sines, or even when using a floating point representation with a fixed number of significant digits.
In a sequence of calculations, these rounding errors generally accumulate, and in certain “ill-conditioned” cases, they may make the result meaningless.
Discover how to round off decimal numbers.
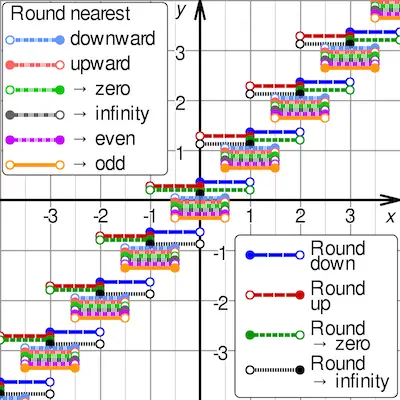
One of the things that you need to keep in mind about rounding numbers is that there are different types of rounding:
- Approximating an irrational number by a fraction. For example, Pi by 22/7.
- Approximating a fraction with periodic decimal expansion by a finite decimal fraction. For example, 5/3 by 1.6667.
- Replacing a rational number by a fraction with a smaller numerator and denominator. For example, 3122/9417 by 1/3.
- Replacing a fractional decimal number by one with fewer digits. For example, 2.1784 dollars by 2.18 dollars.
- Replacing a decimal integer with an integer with more trailing zeros. For example. 23,217 people by 23,200 people.
- Replacing a value by a multiple of a specified amount. For example. 27.2 seconds by 30 seconds (a multiple of 15).
Round Half Up And Round Half Down Modes
Round Half Up Mode

According to this rounding rule, the value 23.5 gets rounded to 24, but −23.5 gets rounded to −23.
If it were not for the 0.5 fractions, the roundoff errors introduced by the round to nearest method would be quite symmetric: for every fraction that gets rounded up (such as 0.268), there is a complementary fraction (namely, 0.732) that gets rounded down, by the same amount.
When rounding a large set of numbers with random fractional parts, these rounding errors would statistically compensate each other, and the expected (average) value of the rounded numbers would be equal to the expected value of the original numbers.
However, the round half up tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded up. This asymmetry introduces a positive bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 higher than the expected value of y. For this reason, round-to-nearest with the round half up rule is also (ambiguously) known as asymmetric rounding.
Learn how to round off whole numbers.
Round Half Down Mode
According to this rounding rule, 23.5 gets rounded to 23, and −23.5 gets rounded to −24.
The round half down tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded down. This asymmetry introduces a negative bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 lower than the expected value of y. For this reason, round-to-nearest with the round half down rule is also (ambiguously) known as asymmetric rounding.